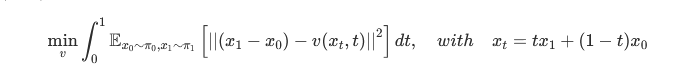AIGC论文阅读——Rectified Flow

Rectified Flow

Rectified Flow的基本思想

用模型去学习两个分布数据点之间的变化速度v，通过$x_{t+1}=x_t+vt,t\in (0,1)$，以实现将源数据转换为目标数据，v通过神经网络学习，并通过多次ReFlow（用训练好的模型生成配对数据进行第二轮的模型训练，模型参数复制上一轮），可以拉直生成轨迹，加快生成速度。

Rectified Flow的思路

给定从两个分布$\pi_0,\pi_1$中的采样，希望找到一个传输映射T使得，当$Z_0 \backsim \pi_0$时，$Z_1=T(Z_0) \backsim \pi_1$。
映射T可以通过以下常微分方程ODE，或者叫流模型，来隐式定义：

$\frac{d\ Z_t}{dt}=v(Z_t,t),Z_0\backsim\pi_0,t\in[0,1].$

可以想象从$\pi_0$里采样出来的$Z_0$是一个粒子，它从t=0时刻开始连续运动，在t时刻以v为速度。知道t=1时刻到达$Z_1$。这里用神经网络来学习v。
上式使用Euler法（或其变种）用离散时间进行近似计算：

$Z_{t+\epsilon}=Z_t+\epsilon v(Z_t,t),$

其中$\epsilon$是一个步长参数，越小越精确，但生成速度就慢。为了用较大的$\epsilon$（例如1）还保持高精度，提出“走直线”。如下图中，蓝色为真实ODE轨迹，绿色为Euler法得到的离散轨迹。

假设从两个分布中各自随机采样，有$x_0\backsim\pi_0,x_1\backsim\pi_1$，这时的$x_0,x_1$并不配对。简单对它们线性插值得到$x_t$:

$x_t=tx_1+(1-t)x_0,t\in[0,1]$,

对它求导得到一个简单的ODE：

$\frac{d\ x_t}{dt}=x_1-x_0$

但这个在前向过程中不可用，因为x1并不知道，因此提出一个可前向模拟的$v(Z_t,t)$来逼近这个导数：

通过上一步，得到的ODE轨迹虽然避免了交叉，但轨迹仍然是弯曲的，这代表生成无法一步实现，因此提出ReFlow方法将轨迹进一步拉直。

首先用两个分布中随机采样的非配对数据训练一个Flow，称为1-Rectified Flow，然后用训练好的模型采样：$x_1=Flow_1(x_0)$，如此得到的(x0,x1)就是比较配对的数据对，用它的参数再去训练一个2-Rectified Flow。

2-Rectified Flow和1-Rectified Flow在训练过程中唯一的区别就是数据配对不同。理论上可以重复Reflow多次，可证明该过程其实是在单调地减小最优传输理论中的传输代价(transport cost)，而且最终收敛到完全直的状态。

当ODE轨迹完全拉直时，就可以通过$x_0 = x_1-v(x_1,1)$一步得到去噪后的图像。